Math for Programmers: Difference of Sets
Last post we discussed union and intersection of sets. These two functions are common and well used, so they are quite important to understand at a deep level, especially if you work with databases on the regular. It can also be helpful to understand these behaviors if you have lots of sets of simple data which need to be combined in a straightforward way.
Difference Explanation
One last, critical, function which is typically used on two or more sets is the difference operation. The difference of sets can be characterized as A - B where the outcome is the set A with all elements shared with set B removed. We can visualize the difference of sets with the following diagram.
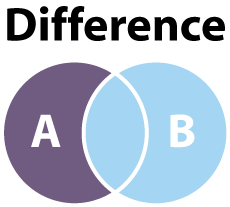
Unlike union and intersection which are commutative, the difference of two sets is not. This means that A ⋂ B and B ⋂ A are the same operation; the same can be said for A ⋃ B and B ⋃ A. The difference A - B is not the same as B - A. We can create a concrete example as follows.
A = {1, 2, 3, 4, 5}
B = {3, 4, 5, 6, 7}
A - B = {1, 2}
B - A = {6, 7}
Clearly these two differences are distinct and different. It is quite helpful to understand the order result of set difference when trying to apply functionality to it. we can create a function, called difference, and apply it to two sets. The action would behave like the following diagram:
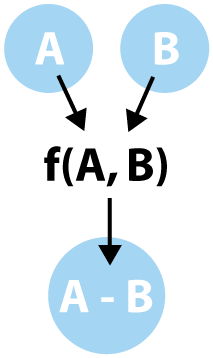
In order to apply our difference function, we need to use a couple of helper functions we introduced in the last post: unique and buildSetMap. These will be important for isolating unique elements and eliminating or keeping them according to our difference functionality.
Predicates as Sets
We can describe a set by way of a predicate function. Effectively, anything which matches the condition of the predicate can be viewed as part of the set while anything which does not match the predicate is not included. A good example of this kind of set partitioning would be the set of even numbers. We could pick values with a function called isEven, which would give us a set like this: {2, 4, 6, 8, …}.
We can describe a more general purpose predicate which simply tests if a value is contained in a set built by our buildSetMap function. The behavior would be simple: test that any value which is provided exists in our set and does not resolve to undefined. Let’s have a look.
function isInSet (set, value){
return typeof set[value] !== 'undefined';
}
We can, now, easily test if a value is contained in a set. This simplifies our problem significantly. Now all we really care about to take a difference is whether a given value is not contained in our set; i.e. then it is part of the difference.
Javascript has a function, filter, which is very closely related to both the intersection and difference of sets. If we choose a predicate which includes all values contained in a set, filter will return the intersection of the set of all values which match our predicate value and the set of values we are testing. If, on the other hand, we use a predicate which only keeps values which are NOT in the set, we get the difference instead.
We can use the factory pattern to keep our code clean and readable, while building a useful difference predicate function. Let’s have a look at the code that makes this work.
function diffFactory(set, value) {
return function (value) {
return !isInSet(set, value);
};
}
Implementing Difference Function
Now we are ready to take the difference of two sets. We have a difference predicate factory, a unique function and a buildSetMap function. Bringing filter into the mix means the code almost writes itself. Let’s build our difference algorithm.
function difference(lista, listb) {
return unique(lista).filter(diffFactory(buildSetMap(listb)));
}
This difference function will produce the difference of any two lists of primitive values. This means our original example of A - B can be done with a small, easy to read line of code; difference(A, B);.
Symmetric Difference Explanation
There is another difference operation which has a special name in computer science, the symmetric difference. Mathematically a symmetric difference can be written one of two ways, (A - B) ⋃ (B - A) or (A ⋃ B) - (A ⋂ B). Both of these operations resolve the same way, which can be visualized by the following diagram.

To make this more clear, let’s have a look at a concrete example of a symmetric difference using our original sets A and B.
A = {1, 2, 3, 4, 5}
B = {3, 4, 5, 6, 7}
symmetricDifference(A, B) = {1, 2, 6, 7}
What all of this really means is the symmetric difference takes everything from sets A and B and excludes the elements they share. A common example is a graph of students taking Math and English but none of the students which are taking both. We can create a function symmetricDifference which performs this operation and lives between the definition of sets A and B and the resulting set.
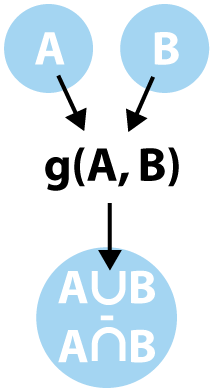
Symmetric Difference Implementation
To create our implementation, I opted for the difference of the union and intersection of A and B. This means we will first compute the union and intersections of our two sets and then take the difference of the two resulting sets.
function symmetricDifference(lista, listb) {
return difference(union(lista, listb), intersect(listb, lista));
}
Once again we see the code practically writes itself. Since we already have functions to perform each of these operations on their own, all we have to do is simply chain them together in a meaningful way and our output simply emerges with nearly no effort at all.
Summary
This closes up the introduction of basic sets and operations including algorithms for acting on lists as sets of data. We discussed how lists and maps relate to sets, what a union and intersection are as well as how to write linear implementation of union and intersection algorithms. We addressed how sets can be defined conceptually with predicate functions and how they interact with concrete sets of data in our programs. Finally, we looked at the difference and symmetric difference operations as well as functions which perform our difference functions in linear time. With all of this closed up, we are ready to start performing more complex manipulations of data using higher order functions which we will discuss in upcoming posts. Until then, keep your code clean and use sets to make your programs better!